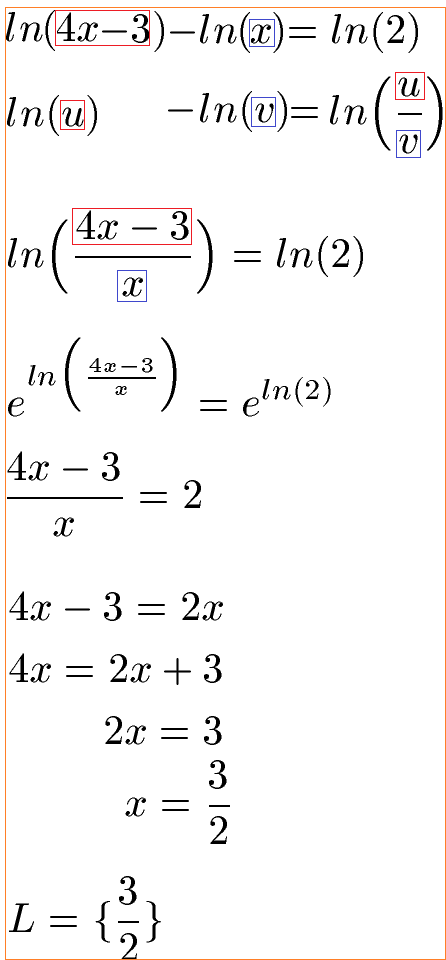Antwort Was bestimmt man mit dem Logarithmus? Weitere Antworten – Für was verwendet man Logarithmus
Logarithmen können wir im Alltag entdecken: Zum Beispiel beim pH-Wert (Maß für den sauren oder basischen Charakter einer wässrigen Lösung, siehe Berechnungen unten) und der Dezibel-Skala (Maß für die Lautstärke). Oder benutzt sie einfach, wenn es um eure Finanzplanung geht, wie beim Zinseszins gezeigt.Was ist der Logarithmus Wer eine Zahl logarithmiert, sucht den Exponenten zu einer bestimmten Basis, etwa zur Basis 10. Dann muss 10 hoch dieser Exponent genau die vorgegebene Zahl ergeben. Ein Beispiel: Der Logarithmus von 100 ist 2, denn 102 ergibt 100.Anwendung. Mit dem Logarithmus lassen sich Exponentialgleichungen lösen. Auch bestimmte Stellen von Exponentialfunktionen werden mithilfe des Logarithmus gefunden.
Wann muss ich den Logarithmus anwenden : Du verwendest ihn immer dann, wenn du den Exponenten x zu einer Basis 2 suchst. So kannst du zum Beispiel berechnen, dass du die 2 sechsmal mit sich selbst multiplizieren musst, um 64 zu erhalten. Dafür verwendest du log zur Basis 2 auf deinem Taschenrechner. Für diesen log Basis 2 gibt es verschiedene Schreibweisen.
Was ist der log von 2
Binärer Logarithmus
| x | -3 | 2 |
|---|---|---|
| 2x | ⅛ | 4 |
Was ist der Logarithmus von 9 : Natürlicher und Dekadischer Logarithmus
| x | log₁₀x | logₑx |
|---|---|---|
| 9 | 0,954243 | 2,197225 |
| 10 | 1 | 2,302585 |
| 20 | 1,30103 | 2,995732 |
| 30 | 1,477121 | 3,401197 |
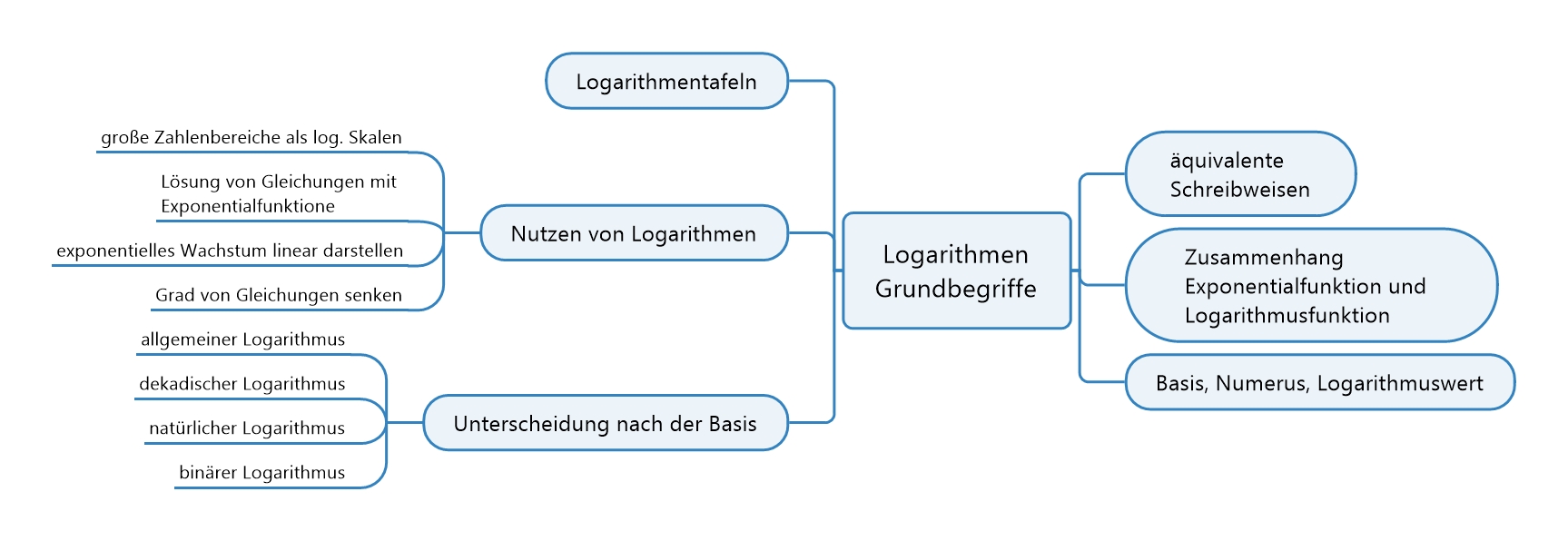
Als Logarithmus (Plural: Logarithmen; von altgriechisch λόγος lógos, „Verständnis, Lehre, Verhältnis“, und ἀριθμός, arithmós, „Zahl“) einer Zahl bezeichnet man den Exponenten, mit dem eine vorher festgelegte Zahl, die Basis, potenziert werden muss, um die gegebene Zahl, den Numerus, zu erhalten.
Durch die logarithmische Darstellung werden Zusammenhänge im Bereich der kleinen Werte besser überschaubar. Verschiedene mathematische Zusammenhänge können durch logarithmische Darstellung besser verdeutlicht bzw. erst erkennbar gemacht werden.
Was ist der log von 4
Natürlicher und Dekadischer Logarithmus
| x | log₁₀x | logₑx |
|---|---|---|
| 4 | 0,60206 | 1,386294 |
| 5 | 0,69897 | 1,609438 |
| 6 | 0,778151 | 1,791759 |
| 7 | 0,845098 | 1,94591 |
Die Logarithmusfunktion y = logb (x) ist die Umkehrfunktion der Exponentialfunktion y = bx. Deshalb sind die Graphen Spiegelbilder an der Geraden y = x. Du bezeichnest die Umkehrfunktion mit f-1. Die Logarithmusfunktionen haben unabhängig von der Wahl der Basis noch weitere gemeinsame Eigenschaften.Logarithmische Skalen ermöglichen dir eine übersichtlichere Darstellung von Kurvenverläufen vor allem dann, wenn sie sich über sehr große Zahlenbereiche erstrecken. 2 Zeichne eine Gerade durch die beiden Punkte A(3|– 1) und B(– 2|5) und ermittle grafisch und rechnerisch die Steigung der Geraden.
Dekadischer Logarithmus
Das bekannteste Logarithmen-System ist das des dekadischen Logarithmus. Der dekadische Logarithmus zeichnet sich dadurch aus, dass seine Basis immer den Wert 10 besitzt. Anstatt des ausführlichen Ausdrucks \log_{10}(b) schreibt man \lg{b}.
Was ist der Unterschied zwischen linear und logarithmisch : Während bei der linearen Variante die Skalierung der vertikalen Achse in gleichgroßen absoluten Abständen erfolgt – beispielsweise in Tausenderschritten –, bilden logarithmische Charts prozentuale Veränderungen ab.
Wie lauten die wichtigsten Rechenregeln für log : Es gibt folgende wichtige Logarithmengesetze:
- Produktregel: logbx + logbz = logb(x·z)
- Quotientenregel: logbx − logbz = logb(x/z)
- Potenzregel: logb(xz) = z·logb(x)
- Potenzregel: logb(n-sqrt(z))=1/n·logb(z)
- Basiswechsel: logb(x)=(loga(x))/(loga(b))
In welcher Klasse macht man Logarithmen
Logarithmen: Gymnasium Klasse 10 – Mathematik.
Es gibt folgende wichtige Logarithmengesetze:
- Produktregel: logbx + logbz = logb(x·z)
- Quotientenregel: logbx − logbz = logb(x/z)
- Potenzregel: logb(xz) = z·logb(x)
- Potenzregel: logb(n-sqrt(z))=1/n·logb(z)
- Basiswechsel: logb(x)=(loga(x))/(loga(b))
Der Logarithmus wird mit "log" bezeichnet. Bei Exponentialfunktionen steht immer eine Zahl b in der Basis und eine Variable x im Exponenten. b hoch x ist dann gleich eine Zahl. Mit dem Logarithmus kannst du herausfinden, mit welchem Exponenten x zur Basis b du die Zahl herausbekommst.
Warum wird Logarithmiert : Der Logarithmus ist eine Rechenoperation, mit der man den (gesuchten) Exponenten einer bekannten Zahl herausfinden kann. Das Logarithmieren ist damit die Umkehroperation zum Potenzieren.