Antwort Wie sieht die Kosinusfunktion aus? Weitere Antworten – Wie sieht eine Kosinusfunktion aus

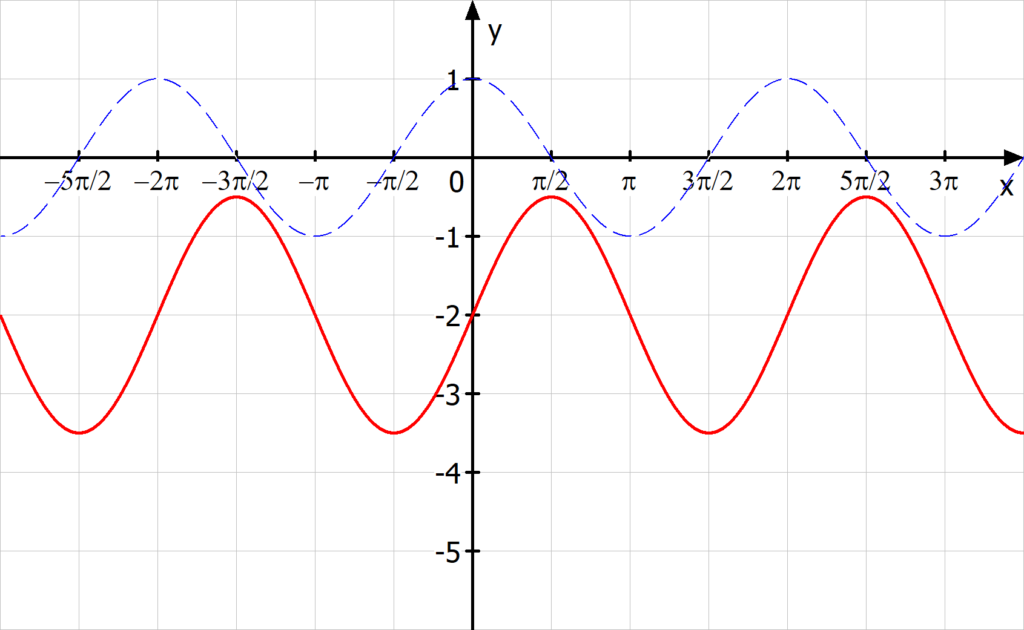
Als allgemeine Gleichung einer Kosinusfunktion wird oft f(x)=a · cos (bx + c) + d bezeichnet. Reelle Zahlen a, b, c und d haben folgende Effekte: a streckt entlang der y-Achse.Die Kosinuskurve verläuft periodisch, das heißt, dass sich ein einzelner Abschnitt immer wieder wiederholt. Man kann auch sagen, dass sich die Funktionswerte y im selben Abstand wiederholen. Eine Wellenbewegung oberhalb und unterhalb der x-Achse entspricht einer kleinsten Periode von 2 \pi.Allgemeine Kosinusfunktion: Die trigonometrische Funktion y = A cos ( B ( x − D ) ) + C .

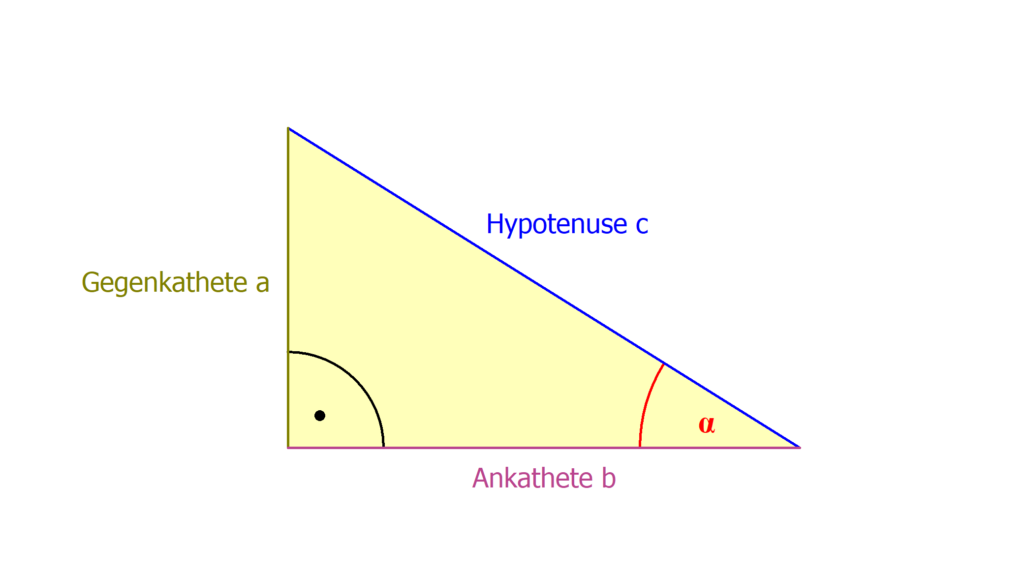
Wie lautet der Cosinus : sin(α)= Gegenkathete / Hypotenuse. cos(α)= Ankathete / Hypotenuse. tan(α)= Gegenkathete / Ankathete.

Wie erkenne ich eine Kosinusfunktion

Kosinusfunktion – Symmetrie

Da du weißt, dass die Kosinusfunktion periodisch ist, kannst du eine weitere Eigenschaft erkennen: Die Kosinusfunktion ist achsensymmetrisch zur y-Achse. Zur Erinnerung: Eine Funktion ist achsensymmetrisch zur y-Achse, wenn gilt: f ( x ) = f ( – x ) .

Wie verwende ich die Kosinusfunktion : Mathematisch wird die Kosinusfunktionsformel in Bezug auf die Seiten eines rechtwinkligen Dreiecks wie folgt geschrieben: cos x = Angrenzende Seite/Hypotenuse = Basis/Hypotenuse , wobei x der spitze Winkel zwischen der Basis und der Hypotenuse ist.

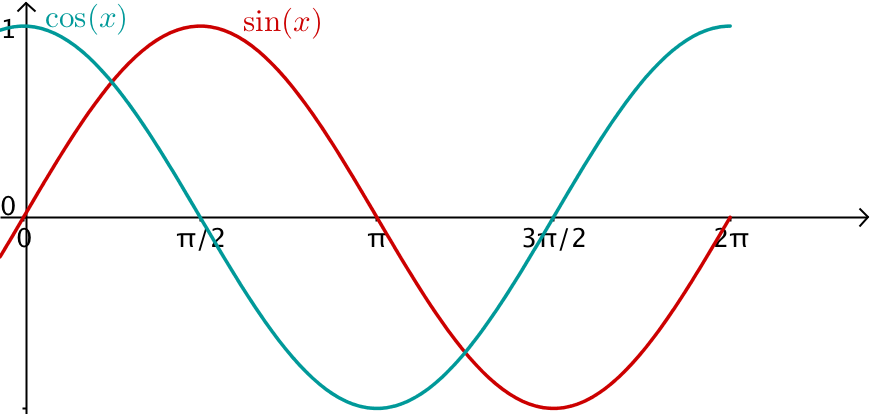
Die bekanntesten periodischen Funktionen sind die trigonometrischen Funktionen. Die Sinusfunktion und die Kosinusfunktion sind periodisch mit der Periode 2 π . Aus ihnen lassen sich weitere periodische Funktionen zusammensetzen, z.B. die Funktionen f ( x ) = a ⋅ sin b x mit der Periode p = 2 π b .

Die Kosinusfunktion (oder Kosinusfunktion) in einem Dreieck ist das Verhältnis der Ankathete zur Hypotenuse . Die Kosinusfunktion ist eine der drei wichtigsten trigonometrischen Hauptfunktionen und selbst das Komplement des Sinus (Co+Sinus).

Wie sieht die Tangensfunktion aus

Die Tangensfunktion ist periodisch, es gilt tanx=tan(x+k⋅π) (k∈Z). Der Funktionsgraph der Tangensfunktion ist punktsymmetrisch zum Ursprung, sie ist also eine sog. ungerade Funktion. Er ist außerdem auch punktsymmetrisch zu allen Nullstellen (weil die Funktion bis nach „±∞“ periodisch ist).Die Kosinusfunktion

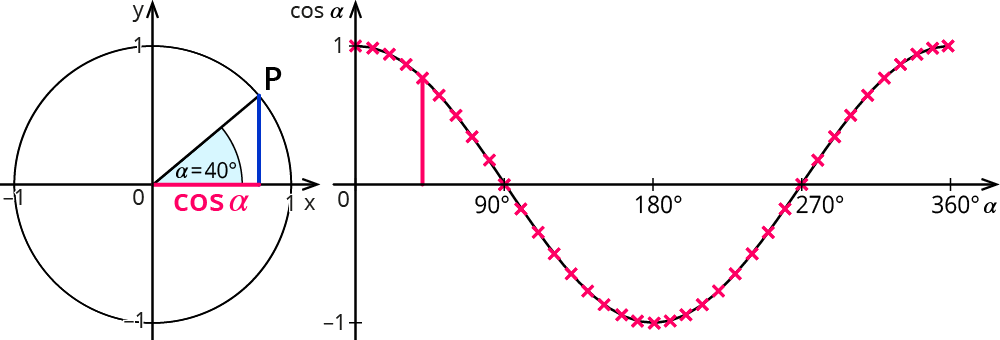
entsteht, wenn man den Kosinus mit Hilfe des Einheitskreises von der Geometrie in die Analysis überträgt. Er erhält nun nicht mehr einen Winkel als Argument, sondern Werte im Bogenmaß (Taschenrechner auf rad stellen!).The general equation for a sine and cosine curve is y = A sin ⁡ ( x − h ) + k and y = A cos ⁡ ( x − h ) + k , respectively. Similar to other function transformations, is the horizontal shift (also called a phase shift), and is the vertical shift.

Der Sinus eines Winkels ist das Verhältnis der Länge der Gegenkathete (Kathete, die dem Winkel gegenüberliegt) zur Länge der Hypotenuse (Seite gegenüber dem rechten Winkel). Der Kosinus ist das Verhältnis der Länge der Ankathete (das ist jene Kathete, die einen Schenkel des Winkels bildet) zur Länge der Hypotenuse.

Wie sieht die Sinusfunktion aus : Als allgemeine Gleichung einer Sinusfunktion wird oft f(x) = a sin (bx + c) + d bezeichnet. Reelle Zahlen a, b, c und d haben folgende Effekte: a streckt entlang der y-Achse.

Wie löst man nach dem Kosinus : Kosinusformeln unter Verwendung des Kosinusgesetzes

Betrachten Sie ein Dreieck ABC, in dem AB = c, BC = a und CA = b. Die Kosinusformeln, die das Kosinusgesetz verwenden, lauten: cos A = (b 2 + c 2 – a 2 ) / (2bc) cos B = (c 2 + a 2 – b 2 ) / (2ac)

Wie lautet Tangens

Tangens: Formeln

Auf diese Formeln kommst du durch Umformung der Grundformel tan(\alpha) = \frac{Gegenkathete}{Ankathete}.

Du siehst daran, dass π π tan ( π ) = – tan ( – π ) = 0 und tan ( 1 ) = – tan ( – 1 ) ≈ 1 , 58 ist.Der genau Wert von cos(90°) cos ( 90 ° ) ist 0 .

Was ist die Kosinusregel in einem Dreieck : Gemäß der Kosinusregel ist das Quadrat der Länge einer beliebigen Seite eines Dreiecks gleich der Summe der Quadrate der Länge der anderen beiden Seiten, subtrahiert mit dem Doppelten ihres Produkts, multipliziert mit dem Kosinus ihres eingeschlossenen Winkels.