Antwort Wie verläuft eine Logarithmusfunktion? Weitere Antworten – Wie verläuft die Logarithmusfunktion

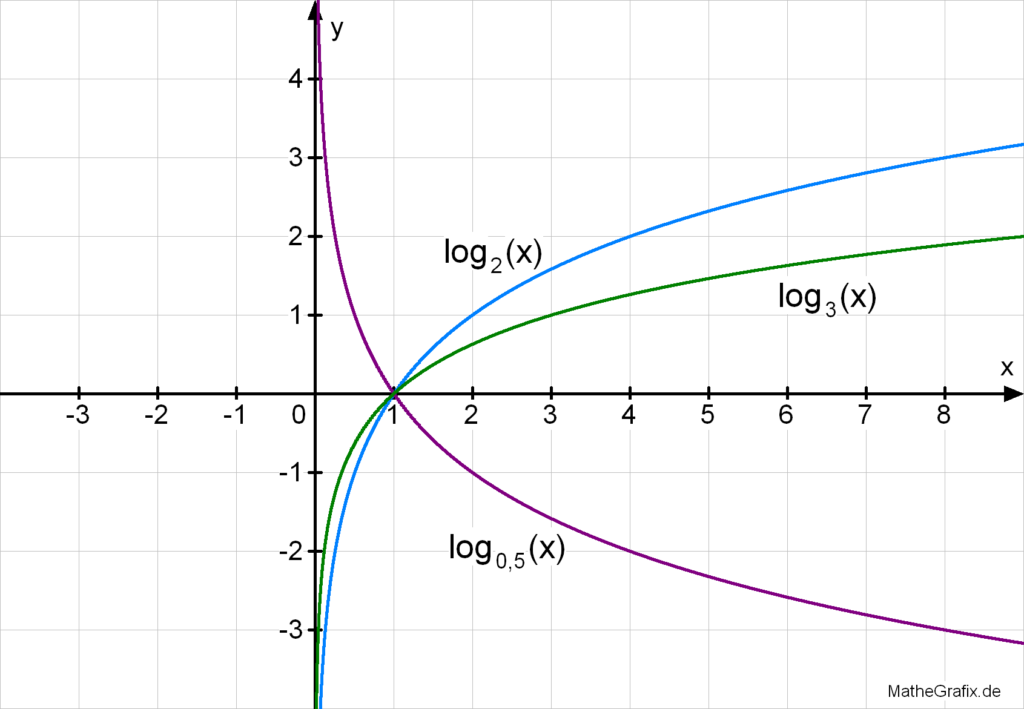
Jede Logarithmusfunktion der Form y=logb(x) verläuft durch den Punkt (b∣1). Der Graph schmiegt sich für b>1 dem negativen und für 0<b<1 dem positiven Teil der y-Achse an. Für b>1: Für x>1 verläuft der Graph oberhalb der x-Achse, für 0<x<1 unterhalb der x-Achse.Die ln-Funktion ist die natürliche Logarithmusfunktion. Der Funktionsgraph verläuft u.a. durch die Punkte P(1|0) und Q(e|1) ≈Q(2,7|1). Die Funktionswerte (y-Werte) der Funktion nehmen alle reellen Zahlen an, der Graph verläuft also oberhalb sowie unterhalb der x-Achse.Als Logarithmus (Plural: Logarithmen; von altgriechisch λόγος lógos, „Verständnis, Lehre, Verhältnis“, und ἀριθμός, arithmós, „Zahl“) einer Zahl bezeichnet man den Exponenten, mit dem eine vorher festgelegte Zahl, die Basis, potenziert werden muss, um die gegebene Zahl, den Numerus, zu erhalten.

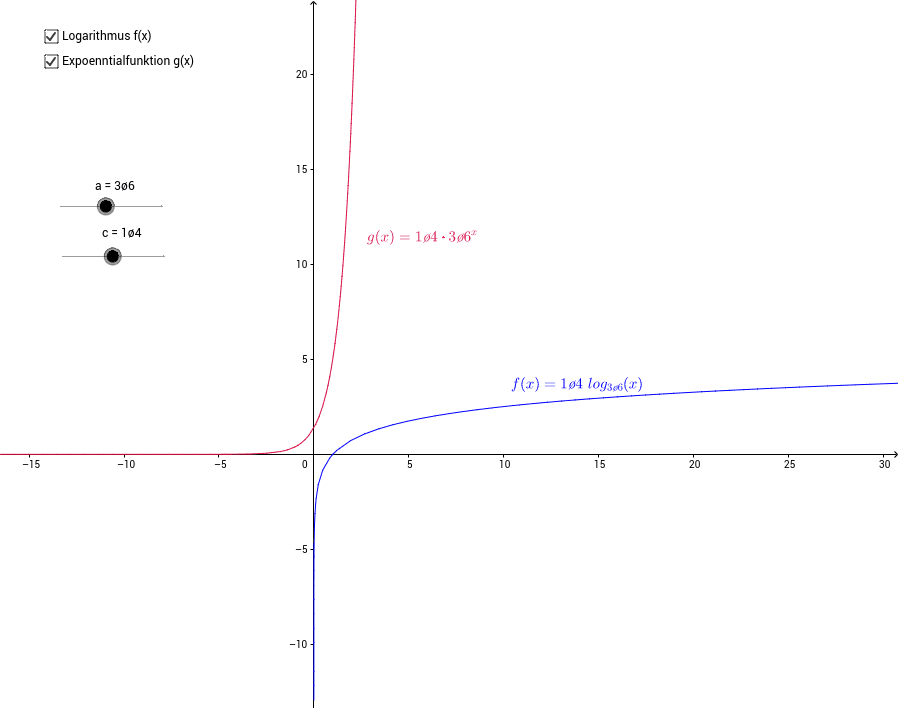
Was macht die log Funktion : Die Logarithmusfunktion y = logb (x) ist die Umkehrfunktion der Exponentialfunktion y = bx. Deshalb sind die Graphen Spiegelbilder an der Geraden y = x. Du bezeichnest die Umkehrfunktion mit f-1. Die Logarithmusfunktionen haben unabhängig von der Wahl der Basis noch weitere gemeinsame Eigenschaften.

Wie lauten die wichtigsten Rechenregeln für log

Es gibt folgende wichtige Logarithmengesetze:

• Produktregel: logbx + logbz = logb(x·z)
• Quotientenregel: logbx − logbz = logb(x/z)
• Potenzregel: logb(xz) = z·logb(x)
• Potenzregel: logb(n-sqrt(z))=1/n·logb(z)
• Basiswechsel: logb(x)=(loga(x))/(loga(b))

Was rechnet man mit dem Logarithmus : Anwendung. Mit dem Logarithmus lassen sich Exponentialgleichungen lösen. Auch bestimmte Stellen von Exponentialfunktionen werden mithilfe des Logarithmus gefunden.

Beispiele der Logarithmusgesetze

• Erstes Logarithmusgesetz: log 7 (3 · 8) = log 7 (3) + log 7 (8)
• Zweites Logarithmusgesetz: log4 (4/5) = log 4 (4) – log 4 (5)
• Drittes Logarithmusgesetz: log3 (75) = 5 · log3 (7)
• Viertes Logarithmusgesetz: 1/3 · log3 (96) = log3 (3√96)

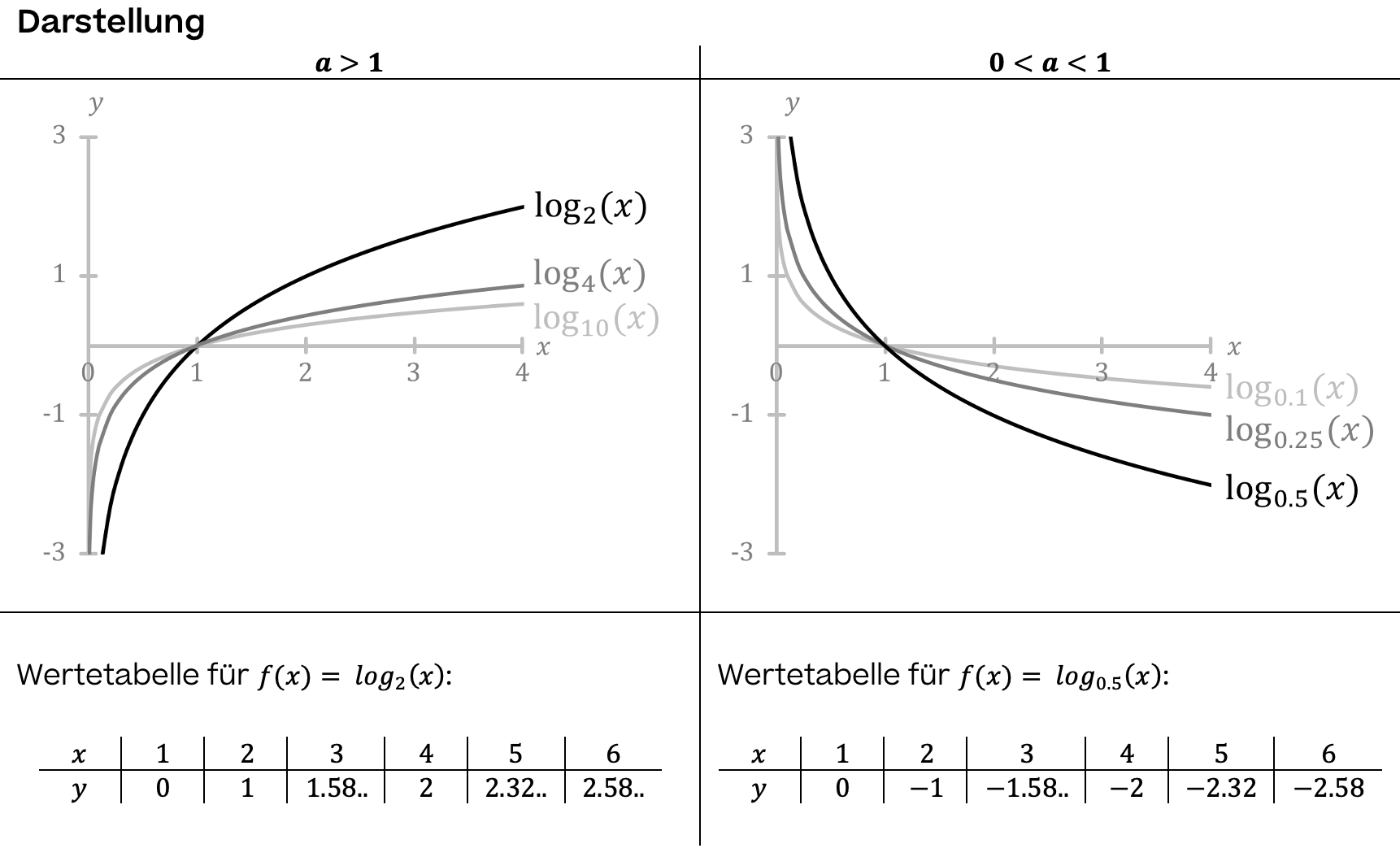
Der natürliche Logarithmus von null ist nicht definiert.

Was ist ein Logarithmus Beispiel

Der Logarithmus ist der Exponent

2x=8 → x=log28 ("x ist der Logarithmus zur Basis 2 von 8") und natürlich gilt x=3 da 23=8. 5x=25→ x=log525 ("x ist der Logarithmus zur Basis 5 von 25") und natürlich gilt x=2 da 52=25 ist.Natürlicher und Dekadischer Logarithmus

x	log₁₀x	logₑx
4	0,60206	1,386294
5	0,69897	1,609438
6	0,778151	1,791759
7	0,845098	1,94591

Der Logarithmus einer Zahl gibt an, zu welcher Potenz die Basis erhöht werden muss, um die gegebene Zahl zu erhalten. In der Finanzanalyse wird der Logarithmus häufig verwendet, um die Rendite von Aktien oder anderen Finanzinstrumenten zu berechnen.

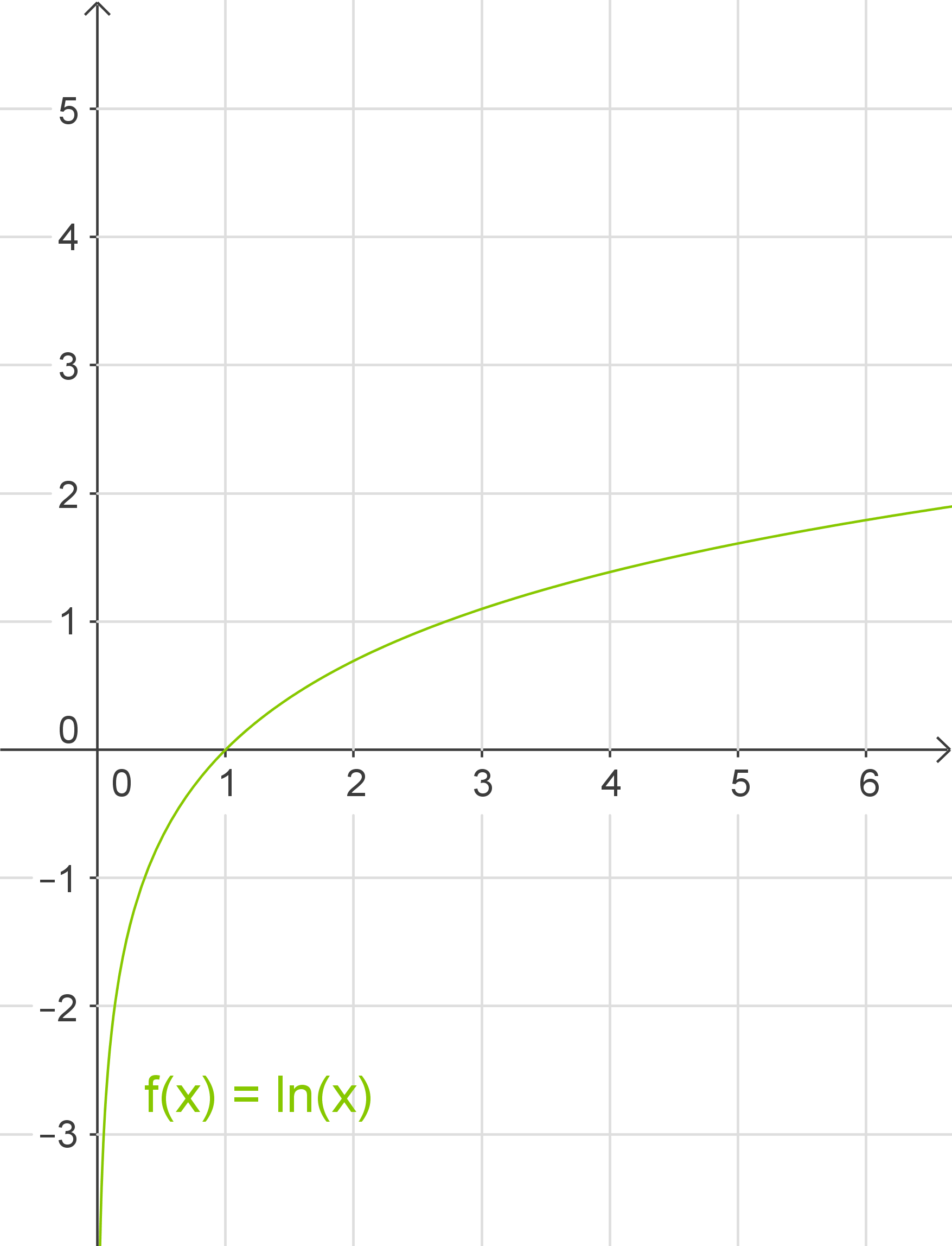
Binärer Logarithmus

x	-3	2
2x	⅛	4

Wie löst man eine Logarithmusgleichung : Um den Logarithmus nach x aufzulösen, wandelst du die Gleichung in eine Potenz um. Dazu schreibst du die Basis x hoch den Exponenten 2 auf. Das ergibt den Logarithmanden 16. Jetzt kannst du die Wurzel ziehen und du hast x aufgelöst!

Was berechnet man mit dem Logarithmus : Der Logarithmus ist eine Rechenoperation, mit der man den (gesuchten) Exponenten einer bekannten Zahl herausfinden kann. Das Logarithmieren ist damit die Umkehroperation zum Potenzieren.

Was ist der log von 1

log 1. Anders sieht es für den Logarithmus von 1 aus. Dieser ist nämlich immer Null, ganz unabhängig von der Basis. Das lässt sich mit den Potenzgesetzen erklären, denn für jede Zahl ist x0 = 1.

Der ln 1 ist eine besondere Stelle. Hier ist der natürliche Logarithmus nämlich gerade Null. Erinnere dich an die Potenzgesetze, besonders an die Regel x0=1. Eine Zahl hoch Null ergibt also Eins.Algebra Beispiele

Die logarithmische Basis 3 von 3 ist 1 .

Was ist der log von 9 : Natürlicher und Dekadischer Logarithmus

x	log₁₀x	logₑx
9	0,954243	2,197225
10	1	2,302585
20	1,30103	2,995732
30	1,477121	3,401197