Antwort Wie viele Wendepunkte kann eine Funktion haben? Weitere Antworten – Kann eine Funktion 2 Wendepunkte haben

Funktionen 2. Ordnung, also quadratische Funktionen z.B. f(x)=x² können keine Wendepunkte haben, da sich die Krümmung des Graphen nicht ändert. Funktionen 3. Ordnung, also kubische Funktionen haben immer einen Wendepunkt.Jede Polynomfunktion, die genau zwei lokale Extremstellen hat, hat mindestens eine Wendestelle. Jede Polynomfunktion, deren Grad größer als 3 ist, hat mindestens eine lokale Extremstelle. Jede Polynomfunktion dritten Grades hat genau eine Wendestelle. Jede Polynomfunktion vierten Grades hat mindestens eine Nullstelle.Ortskurve Definition. Zu einer Funktionenschar gehören unendlich viele Funktionen. Die Extrempunkte und Wendepunkte jeder dieser Funktionen liegen auf einem besonderen Graphen – der jeweiligen Ortskurve.

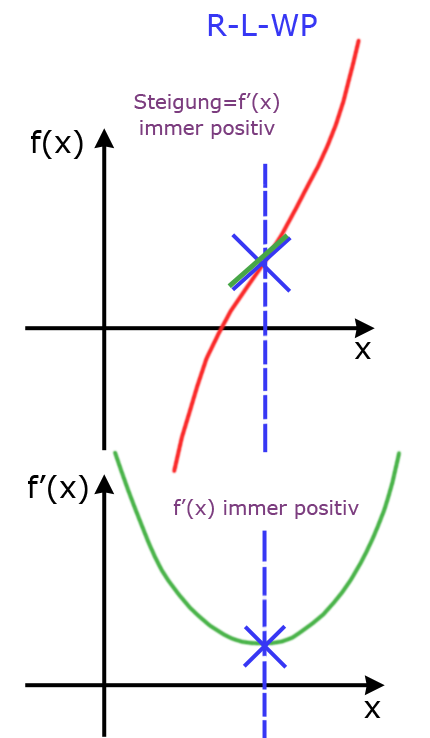
Wann besitzt eine Funktion einen Wendepunkt : Ist die dritte Ableitung ungleich null, hast du einen Wendepunkt berechnet! Wenn die dritte Ableitung gleich 0 ist, kann es sich um einen Sattelpunkt handeln: Das ist auch ein Wendepunkt, jedoch ist beim Sattelpunkt zusätzlich die Steigung, also die erste Ableitung, gleich 0!

Wie viele Wendepunkte kann eine Funktion 5 Grades haben

Ein Polynom fünften Grades hat * fünf Nullstellen, * vier Extremwerte und * drei Wendepunkte!

Wie viele Wendepunkte kann eine Funktion 3 Grades haben : Kubische Funktionen (Grad 3) sind ein Sonderfall: Sie haben immer genau einen Wendepunkt und ihr Graph ist punktsymmetrisch zu diesem Punkt. ganzrationale Funktionen vom Grad haben höchstens − 2 Wendepunkte, da ihre zweite Ableitung den Grad n-2 hat und daher höchstens so viele Nullstellen haben kann.

Wenn der Wert links von der Stelle positiv ist und rechts davon negativ, dann liegt dort ein Wendepunkt, der von einer Linkskurve zu einer Rechtskurve wechselt. Haben die Werte das gleiche Vorzeichen, dann liegt kein Wendepunkt vor.

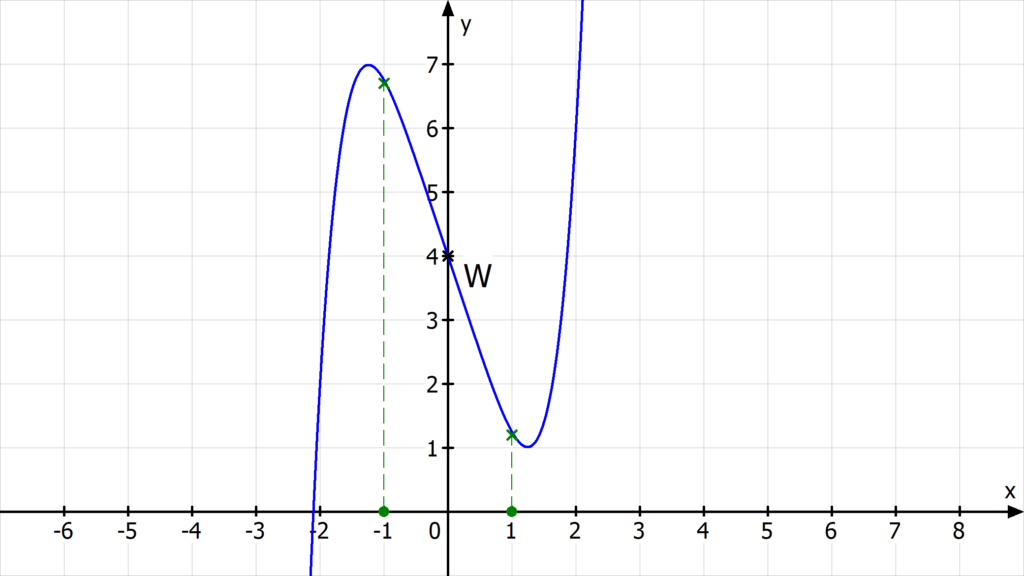
7. f hat mindestens einen Wendepunkt und keinen Extrempunkt.

Welche Funktionen haben keinen Wendepunkt

Bem.: Lineare Funktionen können keinen Wendepunkt haben, weil ihre Krümmung überall Null ist.Was du hier deutlich erkennen kannst, ist, dass die Steigung im Wendepunkt nicht gleich Null ist – es handelt sich also beim Wendepunkt nicht um eine Extremstelle. Dass es sich um einen Wendepunkt handelt, besagt lediglich, dass die Krümmung der Kurve sich verändert. Anders sieht das beim Sattelpunkt aus.Wenn der Wert links von der Stelle positiv ist und rechts davon negativ, dann liegt dort ein Wendepunkt, der von einer Linkskurve zu einer Rechtskurve wechselt. Haben die Werte das gleiche Vorzeichen, dann liegt kein Wendepunkt vor.

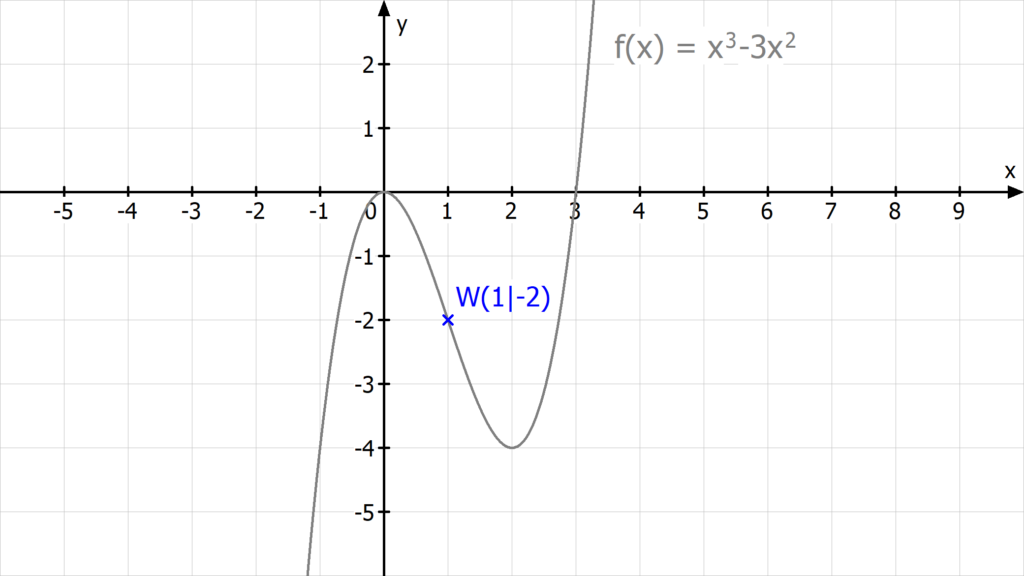
Bedingungen für Wendepunkte

Zu den Wendepunkten gehörender Rechts-Links-Wendepunkt undder Links-Rechts-Wendepunkt bzw. Sattelpunkt.

Wann existiert kein Wendepunkt : Wenn der Wert links von der Stelle positiv ist und rechts davon negativ, dann liegt dort ein Wendepunkt, der von einer Linkskurve zu einer Rechtskurve wechselt. Haben die Werte das gleiche Vorzeichen, dann liegt kein Wendepunkt vor.

Was ist wenn der Wendepunkt 0 ist : Ein Wendepunkt mit waagerechter Tangente ist ein Sattelpunkt bzw. Terrassenpunkt. Wenn eine zweimal differenzierbare Funktion f an der Stelle x0 einen Wendepunkt hat, dann ist ihre zweite Ableitung null (f″(x0)=0) und ihre Krümmung verschwindet dort.

Wie viele Wendepunkte hat eine quadratische Funktion

→Funktionen 2. Ordnung, also quadratische Funktionen z.B. f(x)=x² können keine Wendepunkte haben, da sich die Krümmung des Graphen nicht ändert. Kubische Funktionen haben immer einen Wendepunkt.