Antwort Wo benutzt man Logarithmus? Weitere Antworten – Wo wird Logarithmus benutzt

Er wird im Zusammenhang mit Exponentialfunktionen verwendet. Dekadischer Logarithmus, auch als Zehnerlogarithmus oder Briggsscher Logarithmus bezeichnet, der Logarithmus zur Basis 10. Er wird bei numerischen Rechnungen im Dezimalsystem verwendet.Du verwendest ihn immer dann, wenn du den Exponenten x zu einer Basis 2 suchst. So kannst du zum Beispiel berechnen, dass du die 2 sechsmal mit sich selbst multiplizieren musst, um 64 zu erhalten. Dafür verwendest du log zur Basis 2 auf deinem Taschenrechner. Für diesen log Basis 2 gibt es verschiedene Schreibweisen.Durch die logarithmische Darstellung werden Zusammenhänge im Bereich der kleinen Werte besser überschaubar. Verschiedene mathematische Zusammenhänge können durch logarithmische Darstellung besser verdeutlicht bzw. erst erkennbar gemacht werden.

Was ist Logarithmus Beispiel : Der Logarithmus ist der Exponent

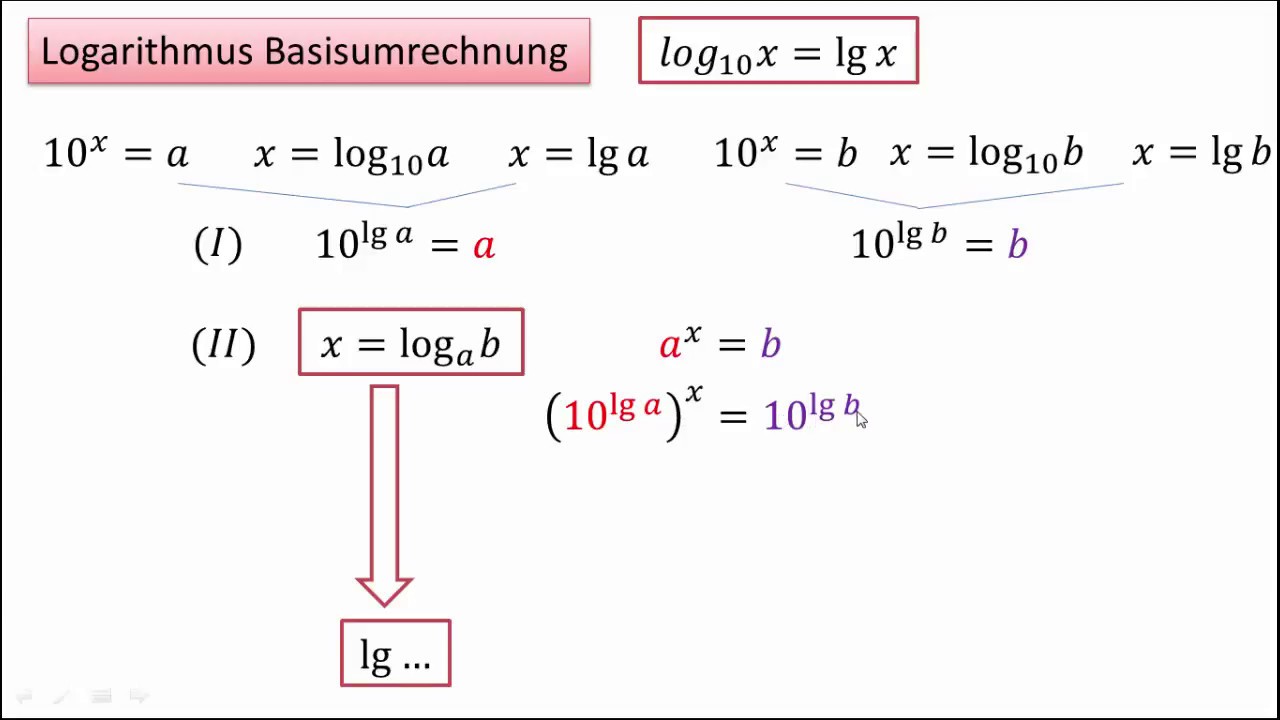
2x=8 → x=log28 ("x ist der Logarithmus zur Basis 2 von 8") und natürlich gilt x=3 da 23=8. 5x=25→ x=log525 ("x ist der Logarithmus zur Basis 5 von 25") und natürlich gilt x=2 da 52=25 ist.

Was sagt Logarithmus aus

Was ist der Logarithmus Wer eine Zahl logarithmiert, sucht den Exponenten zu einer bestimmten Basis, etwa zur Basis 10. Dann muss 10 hoch dieser Exponent genau die vorgegebene Zahl ergeben. Ein Beispiel: Der Logarithmus von 100 ist 2, denn 102 ergibt 100.

Was ist der Logarithmus einfach erklärt : Definition eines Logarithmus

Als Logarithmus einer Zahl bezeichnet man den Exponenten , mit dem eine vorher festgelegte Zahl, die Basis , potenziert werden muss, um die gegebene Zahl zu erhalten.

Der Logarithmus einer Zahl gibt an, zu welcher Potenz die Basis erhöht werden muss, um die gegebene Zahl zu erhalten. In der Finanzanalyse wird der Logarithmus häufig verwendet, um die Rendite von Aktien oder anderen Finanzinstrumenten zu berechnen.

Die Logarithmusfunktion y = logb (x) ist die Umkehrfunktion der Exponentialfunktion y = bx. Deshalb sind die Graphen Spiegelbilder an der Geraden y = x. Du bezeichnest die Umkehrfunktion mit f-1. Die Logarithmusfunktionen haben unabhängig von der Wahl der Basis noch weitere gemeinsame Eigenschaften.

Wann verwende ich log und ln

ln und log sind die Tasten, die du zum Logarithmus auf dem Taschenrechner findest. ln bezeichnet den natürlichen Logarithmus. Das ist der Logarithmus zur Basis e. Die Taste log ist für den dekadischen Logarithmus, den Logarithmus zur Basis 10.Grundsätzlich werden Logarithmen dort verwendet, wo die Werte enorme Größen annehmen. Der Grund hierfür: Wenn wir 10x als Funktion in ein Koordinatensystem einzeichnen, kommt es entlang der y-Achse schnell zu Problemen, da die Werte riesig werden. Mit jedem Schritt +1 auf der x-Achse erhöht sich der Wert enorm.Wann benutzt man den natürlichen Logarithmus Der natürliche Logarithmus kommt dann zum Einsatz, wenn die Basis e beträgt. Zum Beispiel auch, um die Gleichung ex=4 zu lösen.

Was ist der Logarithmus Wer eine Zahl logarithmiert, sucht den Exponenten zu einer bestimmten Basis, etwa zur Basis 10. Dann muss 10 hoch dieser Exponent genau die vorgegebene Zahl ergeben. Ein Beispiel: Der Logarithmus von 100 ist 2, denn 102 ergibt 100.

Was kann man mit dem Logarithmus berechnen : Anwendung. Mit dem Logarithmus lassen sich Exponentialgleichungen lösen. Auch bestimmte Stellen von Exponentialfunktionen werden mithilfe des Logarithmus gefunden.

Ist log immer 10 : Die Basis eines dekadischen Logarithmus hat immer den Wert 10. Der dekadische Logarithmus findet beispielsweise Anwendung beim Lösen von Exponentialgleichungen, d.h. Gleichungen, bei denen die unbekannte Variable x der Exponent einer Potenz ist.

Wie erkläre ich den Logarithmus

Definition eines Logarithmus

Als Logarithmus einer Zahl bezeichnet man den Exponenten , mit dem eine vorher festgelegte Zahl, die Basis , potenziert werden muss, um die gegebene Zahl zu erhalten.

Binärer Logarithmus

x	-3	2
2x	⅛	4

Natürlicher und Dekadischer Logarithmus

x	log₁₀x	logₑx
4	0,60206	1,386294
5	0,69897	1,609438
6	0,778151	1,791759
7	0,845098	1,94591

Was ist der Logarithmus von 50 : Natürlicher und Dekadischer Logarithmus

x	log₁₀x	logₑx
20	1,30103	2,995732
30	1,477121	3,401197
40	1,60206	3,688879
50	1,69897	3,912023